2D Geometric Constraint Solver.
Table of contents
- Intro
- Problem statement
- Mathematical notation
- Example
- Optimizaion
- Geometric primitives parametrization
- Variable substitution
- Geometric constraints implementation
Intro
I spend a lot of time in MCAD programs like SolidWorks, Onshape, Fusion 360, etc. I’ve always been curious about how they work “under the bonnet”, so I decided to create my own parametric 2D drawing editor with a limited set of geometric primitives (only segments and arcs) and basic geometric constraints. The main problem to be solved is Geometric constraint solving, and for fun I decided to develop my own method of solving this problem without first studying existing approaches.
This is what I ended up with:
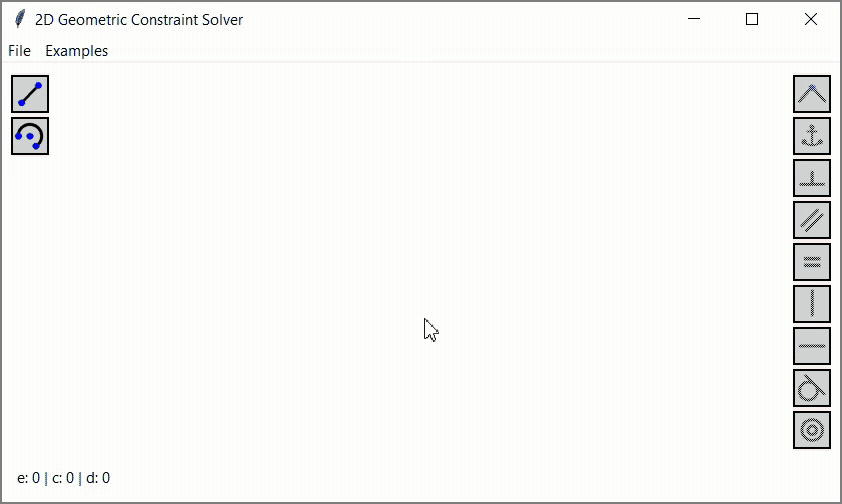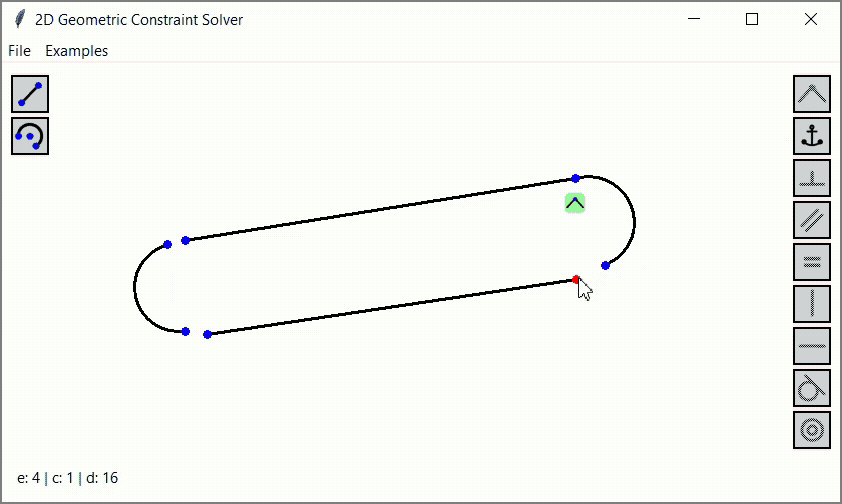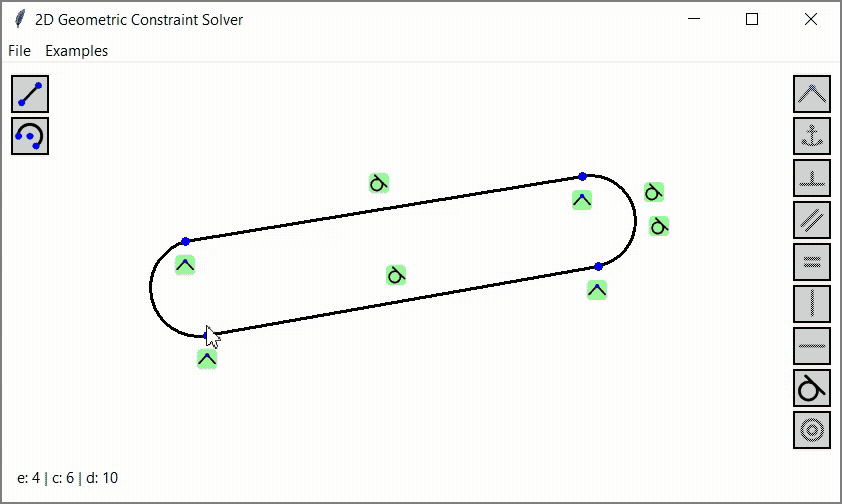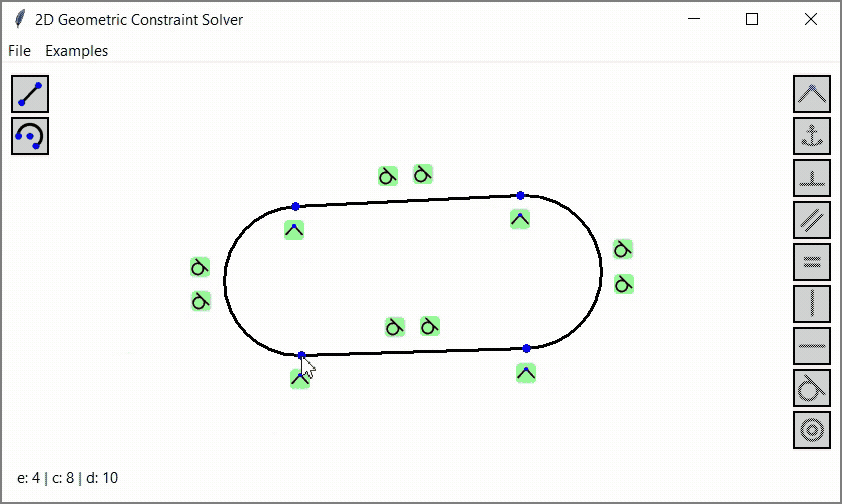
The program is written in Python, the source code is available on GitHub. Below I will try to explain how it all works.
Problem statement
The main functions of the 2D editor to be developed that must be supported are:
- Adding and deleting segments and arcs
- Moving and modifying existing segments and arcs with the mouse, while the program should automatically make sure that existing geometric constraints are not violated
- Imposing new geometric constraints on segments and arcs and deleting existing geometric constraints
Geometric constraints that must be supported:
- COINCIDENCE: point coincidence
- PARALLELITY: segments parallelity
- PERPENDICULARITY: segments perpendicularity
- EQUAL_LENGTH_OR_RADIUS: equal length of segments or equal radius of arcs
- FIXED: fixed points
- HORIZONTALITY: points horizontality
- VERTICALITY: points verticality
- TANGENCY: tangency of an arc and a segment or tangency of two arcs
- CONCENTRICITY: arcs concentricity
To understand how this all works, let’s look at an example:
Mathematical notation
Here are some notations that will be used next:
- $x$ – scalar
- $\vec{y}$ – vector in the mathematical sense
- $\vec{f}()$ – vector-valued function
- $\overline{z}$ – vector in the geometric sense
Example
Let’s say we have two segments, $AB$ и $BC$. We also have these geometric constraints:
- $AB$ and $BC$ are perpendicular to each other
- $AB$ and $BC$ have the same length
Let’s say that at time $t_0$ the system was in the solved state, all geometric constraints were satisfied, this state corresponds to segments $A_0B_0$ and $B_0C_0$ in the picture below. Then, using the mouse, we instantly changed the position of the point $C_0$ belonging to the segment $B_0C_0$, after which this point moved to the position $C’$:
Next, the solver must work to find new (corresponding to time $t_1$) positions of all segments, which actually means finding points $A_1$, $B_1$ and $C_1$. The solver has two tasks:
- It is necessary that point $C_1$ be as close as possible to point $C’$. Sometimes (but not always) it is possible to ensure the coincidence of these points
- It is necessary that all existing geometric constraints are satisfied
This is what it will look like after the solver completes its work:
Let’s write down the solver tasks defined above in more formal language:
\[dist(C', C_1) \rightarrow min\] \[\begin{cases} A_1B_1 \perp B_1C_1\\ \norm{\overline{A_1B_1}} = \norm{\overline{B_1C_1}} \end{cases} \Rightarrow \begin{pmatrix} dot(\overline{A_1B_1}, \overline{B_1C_1}) \\ \norm{\overline{A_1B_1}} - \norm{\overline{B_1C_1}} \end{pmatrix} =0\]In what we get, we can see a special case of the nonlinear programming problem. The general form of the nonlinear programming problem is as follows:
\[\begin{array}{rl} \min _\vec{x} & f(\vec{x}) \\ \text { subject to } & \vec{h}(\vec{x}) \geq 0 \\ & \vec{g}(\vec{x})=0 . \end{array}\]The function $\vec{h}(\vec{x})$ describes inequality constraints, $\vec{g}(\vec{x})$ describes equality constraints. We have only equality constraints, so the expressions take the following form:
\[\begin{array}{rl} \min _\vec{x} & f(\vec{x}) \\ \text { subject to } & \vec{g}(\vec{x})=0. \end{array}\]Let’s explicitly express the vector $\vec{x}$:
\[\vec{x}= \begin{pmatrix} A_x & A_y & B_x & B_y & C_x & C_y \end{pmatrix} ^\intercal\]Let’s explicitly express the $f(\vec{x})$ through the components of the vector $\vec{x}$:
\[f(\vec{x})=dist(C', C_1)=\sqrt{(C'_x - C_{1x})^2 + (C'_y - C_{1y})^2}\]Let’s explicitly express the $\vec{g}(\vec{x})$ through the components of the vector $\vec{x}$:
\[\vec{g}(\vec{x})= \begin{pmatrix} dot(\overline{A_1B_1}, \overline{B_1C_1}) \\ \norm{\overline{A_1B_1}} - \norm{\overline{B_1C_1}} \end{pmatrix} = \begin{pmatrix} (B_{1x} - A_{1x}) \cdot (C_{1x} - B_{1x}) + (B_{1y} - A_{1y}) \cdot (C_{1y} - B_{1y}) \\ \sqrt{(B_{1x} - A_{1x})^2 + (B_{1y} - A_{1y})^2} - \sqrt{(C_{1x} - B_{1x})^2 + (C_{1y} - B_{1y})^2} \end{pmatrix}\]Now that we have formulated the nonlinear programming problem, we can talk about how to solve it.
Optimizaion
I decided not to implement the optimization algorithms myself, but to use the existing Python package scipy.optimize. In particular, from this package we will need the function minimize. This function is interesting because it takes as input a parameter that defines the solver’s type. I have tried different types, and the “SLSQP” variant proved to be the best.
Now, I think the basic program’s working principle is clear. But we also need to discuss some subtleties:
Geometric primitives parametrization
From the above example, it is clear that we need to be able to transform our system from a set of segments and arcs to a vector of numbers ($\vec{x}$) and back again. Such a transformation is called a parameterization. To parameterize a system, we need to parameterize its components and combine the results. Thus, we need to be able to parameterize segments and arcs.
For a segment, we can use the most obvious and simple method, just like in the example. Let’s say we have a segment $AB$, then the vector $\vec{x}$ corresponding to it will have the form:
\[\vec{x}_{AB}= \begin{pmatrix} A_x & A_y & B_x & B_y \end{pmatrix} ^\intercal\]There are several parameterization options for arcs. The most obvious one is probably the set of coordinates of the arc center, radius and two angles, initial and final. However, I found this option to be inconvenient, and it also does not allow me to use the variable substitution trick that will be described later. Therefore, I decided to use another approach:
In this case, to define the arc, the points of its beginning and end, as well as the scalar $d$ are used. It is important to note that the arc is always oriented clockwise. The vector $\vec{x}$ corresponding to the arc will have the form:
\[\vec{x}_{arc}= \begin{pmatrix} P_{1x} & P_{1y} & P_{2x} & P_{2y} & d \end{pmatrix} ^\intercal\]Now let us understand what a scalar $d$ is. Point $O$ is the center of the arc, point $M$ is the middle of segment $P_1P_2$. The vector $\overline{a}$ is equal to the vector $\overline{MO}$. The vector $\overline{n}$ is the normal to the segment $P_1P_2$, it is obtained by normalizing the vector $\overline{P_1P_2}$ and rotating it 90° counterclockwise. The scalar $d$ is calculated as follows:
\[d=dot(\overline{a}, \overline{n})\]Reconstructing the arc from the vector $\vec{x}_{arc}$ is also not a problem. Since the points $P_1$ and $P_2$ are already known, we only need to find the point $O$. In order to do this, we must first find the point $M$ as the center of the segment $P_1P_2$ and then simply shift this point by the vector $(\overline{n} \cdot d)$.
Variable substitution
Geometric constraints that occur very often are the coincidence of points, that is, COINCIDENCE, and the horizontality and verticality of points, HORIZONTALITY and VERTICALITY. Again, let’s look at a small example:
We have two segments, $AB$ and $CD$. We want to impose a geometric constraint of matching points on points $B$ and $C$.
The simplest and most naive way to do this is to simply add two elements to $\vec{g}(\vec{x})$:
\[\vec{g}(\vec{x})= \begin{pmatrix} B_x - C_x \\ B_y - C_y \end{pmatrix}\]The problem with this approach is that there can be a lot of geometric constraints of the COINCIDENCE type. If you take them into account in the above way, it will make the solver’s life very difficult, because there will be a lot of elements in $\vec{g}(\vec{x})$. However, there is a way to avoid this:
Initially, the vector $\vec{x}$ for the system depicted above will have the form:
\[\vec{x}= \begin{pmatrix} A_x & A_y & B_x & B_y & C_x & C_y & D_x & D_y \end{pmatrix} ^\intercal\]Given that points $B$ and $C$ coincide, we can make this substitution:
\[\begin{cases} B_x = C_x = \alpha_0\\ B_y = C_y = \alpha_1\\ \end{cases}\]Then the vector $\vec{x}$ will take the following form:
\[\vec{x}= \begin{pmatrix} A_x & A_y & \alpha_0 & \alpha_1 & D_x & D_y \end{pmatrix} ^\intercal\]The same approach can obviously be used for geometric constraints of type HORIZONTALITY and VERTICALITY.
Now let’s talk about how to implement this approach from the programming point of view. Of course, you can think of many approaches, I will describe mine. The Vars array describes the set of variables included in the vector $\vec{x}$. Let’s also create an array Links and fill it with values -1. This number, -1, will mean that the variable is a “base” variable, i.e. it is directly included in the vector $\vec{x}$:
Now, after adding the geometric constraint of matching points $B$ and $C$, let’s add $\alpha_0$ and $\alpha_1$ to the end of the Vars array. Also, add two -1 numbers to the end of the Links array. And now the main point: replace the values of the Links array corresponding to the variables $B_x$ and $C_x$ with the index of the variable $\alpha_0$, i.e. 8. Also, replace the values of the Links array corresponding to the variables $B_y$ and $C_y$ by the index of the variable $\alpha_1$, i.e. 9:
Now it’s simple. Only those variables that correspond to the value -1 in the Links array are “basic”, i.e. they are directly included in the vector $\vec{x}$. If some variable corresponds to some other number in the Links array, you can easily find the corresponding “base” variable using the described structure.
Geometric constraints implementation
It is quite obvious here, we just need to represent each geometric constraint as a function $\vec{g}(\vec{x})$, which is equal to zero in the case when the geometric constraint is satisfied. Some geometric constraints are described in the Example section, implementation of the rest can be found in the code.






